Software Formula Of Skewness
Pearson has formulas for the moment-kurtosis and the square of the moment skewness ($ beta2$ and $ beta1$) in his 1895 paper, and they're being used in some sense to help describe shape, even though the notion of kurtosis is not particularly developed there. How to find Skewness Excel 2013 Stephanie Glen. Compare Two Lists Using the Vlookup Formula - Duration. Skewness - Duration: 10:20. EurekaWow 254,830 views. 10 Super Neat Ways to.
Troubleshooting
Problem
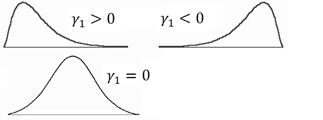
Pearson’s coefficient of skewness is a method developed by Karl Pearson to find skewness in a sample using descriptive statistics like the mean and mode. Skewness is one measure of the shape of a set of data. Note that different formulas for computing skewness and kurtosis can be used. See, for example, the options 'type' of the function kurtosis shown by using?kurtosis after loading the package. Skewness is a measure of the asymmetry of the data around the sample mean. If skewness is negative, the data spreads out more to the left of the mean than to the right. If skewness is positive, the data spreads out more to the right. The skewness of the normal distribution (or any perfectly symmetric distribution) is zero.
I'm running the SPSS EXAMINE procedure (Analyze>Descriptive Statistics>Explore in the menus) using a number of dependent variables. Among the descriptive statistics produced are skewness, kurtosis and their standard errors. I've noticed that the standard errors for these two statistics are the same for all of my variables, regardless of the values of the skewness and kurtosis statistics. Is something wrong?
Resolving The Problem
No, there is nothing wrong here. The standard errors for skewness and kurtosis are solely functions of the sample size, regardless of the values of the statistics themselves. EXAMINE uses LISTWISE deletion of cases with missing values by default, so for a given group, descriptive statistics for all variables will be based on the same number of cases. Thus the SEs for skewness and kurtosis will be the same for all variables.
The variance (squared standard error) of the skewness statistic is computed as:
V_skew = 6*N*(N-1) / ((N-2)*(N+1)*(N+3))
where N is the sample size. The variance of the kurtosis statistic is:
V_kur = 4*(N^2-1)*V_skew / ((N-3)*(N+5))
Internal Use Only
Resolution Status at Transfer: Published - External ; Products: Statistics; Versions: ALL
Related URL
Document Information
Modified date:
16 June 2018
The skewness is a parameter to measure the symmetry of a data set and the kurtosis to measure how heavy its tails are compared to a normal distribution, see for example here.
scipy.stats provides an easy way to calculate these two quantities, see scipy.stats.kurtosis and scipy.stats.skew.
In my understanding, the skewness and kurtosis of a normal distribution should both be 0 using the functions just mentioned. That is, however, not the case with my code:
The output is:
excess kurtosis of normal distribution (should be 0): -0.307393087742
skewness of normal distribution (should be 0): 1.11082371392
What am I doing wrong ?
The versions I am using are
MSeifertSoftware Formula Of Skewness Formula
2 Answers
These functions calculate moments of the probability density distribution (that's why it takes only one parameter) and doesn't care about the 'functional form' of the values.
These are meant for 'random datasets' (think of them as measures like mean, standard deviation, variance):
Free textures for imvu developers. which gives:
changing the number of random values increases the accuracy:
Leading to:
In your case the function 'assumes' that each value has the same 'probability' (because the values are equally distributed and each value occurs only once) so from the point of view of skew and kurtosis it's dealing with a non-gaussian probability density (not sure what exactly this is) which explains why the resulting values aren't even close to 0:
You are using as data the 'shape' of the density function.These functions are meant to be used with data sampled from a distribution.If you sample from the distribution, you will obtain sample statistics that will approach the correct value as you increase the sample size.To plot the data, I would recommend a histogram.
Output:
Unless you are dealing with an analytical expression, it is extremely unlikely that you will obtain a zero when using data.
Juan LeniJuan Leni